Доказать, что если отрезок, соединяющий середины противоположных сторон четырехугольника, равен полусумме двух других сторон, то этот четырехугольник есть трапеция.

Пусть ABCD — данный четырехугольник и точки М, N являются серединами сторон, соответственно, АВ и CD.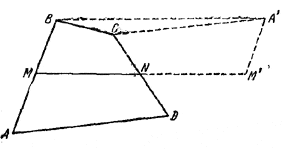

Повернем четырехугольник AMND в плоскости рисунка вокруг вершины N на 180°. Тогда вершина D совпадает с С, а вершины М, А займут положение M', А'. При этом точки М, N, М' расположатся на одной прямой и, кроме того, будет М'А' || MB и М'А' = MB. Поэтому МВА'М'— параллелограмм и A'B = M'M = 2MN.
Так как, по условию BC + AD = 2MN, то ВС + СA' = A'В. Следовательно, точка С лежит на отрезке А'В: в противном случае в \(\Delta\)ВСA' мы имели бы ВС + СА' > А'В. Отсюда следует, что ВС || MN || AD, т. е. ABCD — трапеция.