Из точки, лежащей вне круга, проведены две секущие, внешние части которых содержат по 2 м. Определить площадь четырехугольника, вершинами которого служат точки пересечения секущих с окружностью, зная, что длина двух его противоположных сторон равна 6 м и 2,4 м.

Так как OB • OA = OC • OD и ОВ = ОС, то ОА = ОD.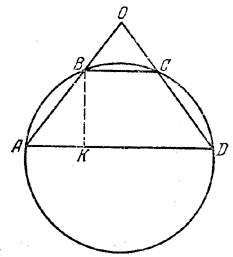

Противоположные стороны AВ и CD четырехугольника ABCD равны; значит, данные длины 6 ми 2,4 м относятся к сторонам AD и BС (AD = 6 м, BС = 2,4 м). Прямые BC и AD, отсекающие на сторонах угла AOD равные отрезки, параллельны, так что четырехугольник ABCD - трапеция (равнобочная). Из подобия треугольников ВОС и AOD находим

ВО : АО = ВС : AD,

откуда

значит, AВ = 3 м. Теперь находим высоту трапеции

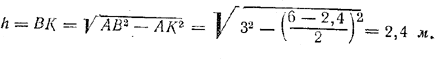
Oтв. S = 10,08 м².