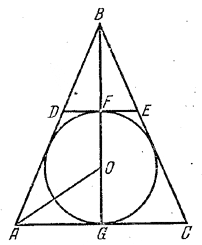
Дан равнобедренный треугольник с основанием 2а и высотой h. В него вписана окружность, и к ней проведена касательная, параллельная основанию. Найти радиус окружности и длину отрезка касательной, заключенного между сторонами треугольника.
Площадь S треугольника ABC равна произведению его периметра 2а + 2 √a2+ h2на r/2 (r - радиус вписанной окружности):S= (а + √a2+ h2)r.
С другой стороны,
S = 1/2 AС • BG= ah.
Приравнивая эти два выражения, находим
![]()
Отрезок DE находим из пропорции
DE : AC = BF : BG,
где
4C = 2a, BF = h -2r и BG = h.
Замечание. Величину r можно найти еще так: прямая АО eсть биссектриса угла А. Значит, отрезки GO = r и OB = h - r пропорциональны сторонам AG и АВ, т. е.
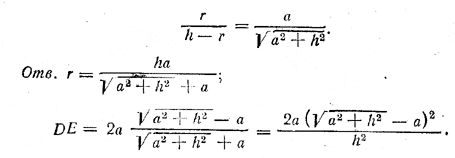
Похожие примеры: