Доказать, что если окружность касается изнутри трех сторон четырехугольника, четвертая сторона которого не пересекает окружности, то сумма четвертой и противоположной сторон меньше суммы двух других сторон четырехугольника.

Пусть сторона AD четырехугольника ABCD не пересекает окружности, а стороны ВС, CD, ВА касаются ее в точках F, E, G.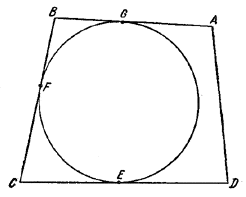

Неравенство

AD + CB < DC + BA

равносильно неравенству

AD < DE + AG,

которое доказано в решении задачи 189.