Доказать, что для любой замкнутой не пересекающей себя ломаной линии в плоскости существует круг, радиус которого составляет ¹/₄ периметра ломаной линии и вне которого нет ни одной точки ломаной.

Выберем точки A и В на ломаной так, чтобы они делили периметр на две равные части. Пусть О — середина отрезка АВ, проведем окружность с центром в О радиуса ^p/₄, где р — периметр всей ломаной.

Докажем, что эта окружность искомая. Допустим противное, т. е. что существует точка М ломаной, лежащая вне построенного круга. Длина той части ломаной, которая содержит М, не меньше, чем АМ + ВМ, т. е. АМ + ВМ < ^p/₂. Но АМ + ВМ > 2МO.

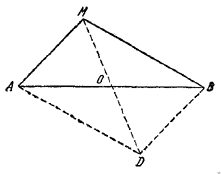
Действительно, из параллелограмма AMBD имеем:

DM = 2MO < BM + BD = AM + BM.

Так как МО > ^p/₄, то из неравенства АМ + ВМ > 2МO следует,

что АМ + ВМ > ^p/₂. Получаем противоречие.