Расстояние между центрами двух пересекающихся кругов радиусов R и r равно d. Найти площадь их общей части.
Искомая площадь равна сумме площадей двух секторов с углами 2α и 2β(рис.) без удвоенной площади треугольника со сторонами R, r, d :
S = R2 α + r2 β — Rd sin α.
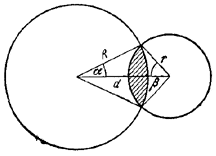
Для определения углов α и βимеем два уравнения:
R sin α= r sin β,
R cos α+ rsin β = d,
решая которые, находим:
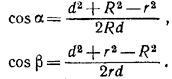
Следовательно,
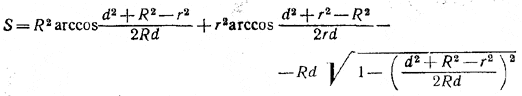
Похожие примеры: