Трехгранный угол пересекается плоскостью по треугольнику ABC. Найти геометрическое место центров тяжести треугольников ABC при условии, что:

1. вершины А и В закреплены;
2. вершина А закреплена.

Случай а). Пусть D - середина отрезка АВ (рис.), С - подвижная точка, Q - центр тяжести \(\Delta\)AВС, Q'-центр тяжести \(\Delta\)ASB. Так как точка Q делит отрезок DC в отношении 1:2, то геометрическое место этих точек есть, очевидно, луч, параллельный ребру SE и проходящий через точку Q'-центр тяжести \(\Delta\)ASВ.

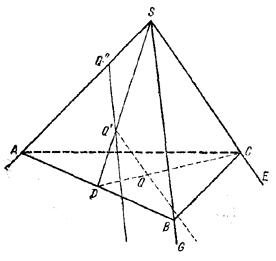
Случай б). Если теперь и точка В перемещается по ребру SG, то центры тяжести Q' треугольников ASB расположатся на луче, параллельном ребру SG и проходящем через точку Q", которая делит отрезок AS в отношении 2:1, считая от А к S, а соответствующие каждому фиксированному положению точки В лучи, рассмотренные в случае а), заполнят сечение трехгранного угла плоскостью, проходящей через точку Q" параллельно ребрам SG и SE.