В треугольник вписан круг радиусом 4 см. Одна из сторон треугольника разделена точкой касания на части, равные 6 см и 8 см. Найти длины двух других сторон.

Для того чтобы найти стороны АВ и ВС треугольника ABC (рис.), достаточно определить EB = BG = x, так как АЕ = AD = 6 см и CG = CD = 8 см.

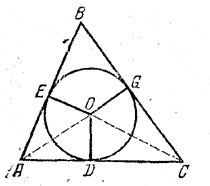
Для этого сравним два выражения для площади треугольника:

S = rp и S =√р(р - а)(р - b)(р - с) ,

где р есть полупериметр треугольника, т. e.

1/2(ЕА + AD + DC + CG + GB + BE) = 1/2 (28 + 2х) = 14 + х.

Получим уравнение

4(14 + х) = √(14 + х) х • 6 • 8 .

Отсюда х = 7 (см).

Ответ: АВ = 13 см; ВС = 15 см.





Похожие примеры:
Через некоторую точку диагонали куба с ребром а перпендикулярно к этой диагонали проведена плоскость. 1) Выяснить, какая фигура получается в сечении этой плоскости с гранями куба. 2) Найти длины отрезков, получающихся в сечении плоскости с гранями куба, в зависимости от расстояния х секущей плоскости от центра симметрии куба О. Смотреть решение→
В основании прямой призмы лежит прямоугольный треугольник с катетом а и противолежащим ему углом α. Через вершину прямого угла нижнего основания проведена плоскость, параллельная гипотенузе, под углом β= 90°— α к противолежащей боковой грани и пересекающая ее. Определить объем части призмы между ее основанием и сечением и боковую поверхность призмы, если известно, что боковая грань, проходящая через катет а, равновелика сечению призмы. Определить, при каком значении угла αплоскость сечения пересекает боковую грань, проходящую через гипотенузу основания. Смотреть решение→
Даны две концентрические сферы радиусов r и R (R > r ). При каком соотношении между R и r можно внутри большей сферы построить правильный тетраэдр так, чтобы три вершины его основания лежали на большей сфере, а три боковые грани касались меньшей сферы?  Смотреть решение→