Даны две концентрические сферы радиусов r и R (R > r ). При каком соотношении между R и r можно внутри большей сферы построить правильный тетраэдр так, чтобы три вершины его основания лежали на большей сфере, а три боковые грани касались меньшей сферы?

Допустим, что задача разрешима. Проведем плоскость A₁B₁C₁ (см. рис. а), касающуюся меньшего шара и параллельную основанию AВС данного тетраэдра. Тетраэдр SA₁B₁C₁ описан около шара радиуса r. Легко найти, что высота его SQ₁ = 4r (см. задачу 249).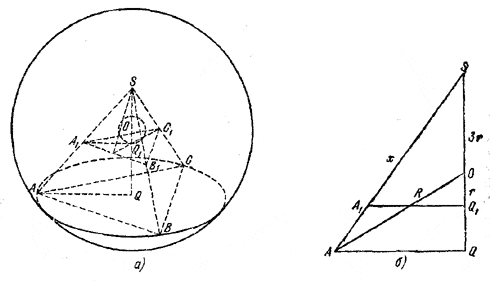

Пусть длина ребра тетраэдра SABC равна х. Тогда отрезок AQ = x ^√3/₃, а высота SQ = x ^√6/₃ .

Далее (см. рис. б) имеем QO = ^x√6/₃ - 3r и из прямоугольного треугольника AQO следует, что

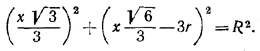
Решив квадратное уравнение, найдем

x_1,2 = r√6 ± √R²- 3r².

В этой формуле следует взять лишь корень со знаком плюс, ибо SA во всяком случае больше, чем 3r, а 3r > r√6 .

Очевидно, что задача возможна при условии R > √3 r