Доказать, что если P, Q, R являются, соответственно, точками пересечения сторон BC, CA, AB (или их продолжений) треугольника ABC с некоторой прямой, то

\(\frac{PB \cdot QC \cdot RA}{PC \cdot QA \cdot RB} = 1\)

Пусть ∠CPQ = α, ∠PQC = β.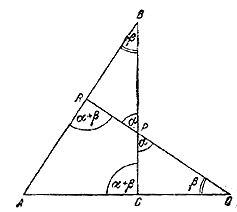

По теореме синусов имеем:

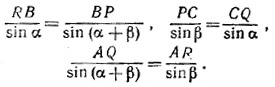
Перемножив эти равенства почленно, получим:

RB•PC•QA=PB•QC•RA.