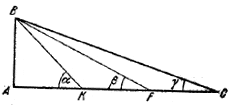
В прямоугольном треугольнике ABC катет АС в 3 раза больше катета AB. Точками К и F катет АС разделен на три равные части. Доказать, что

∠АKB + ∠AFB + ∠ACB = π/2.

Пусть ∠АКВ = α, ∠AFB = β, ∠АСВ = γ.


Имеем α = π/4 , и так как

tg β = 1/2 , tg γ= 1/3 ,

то

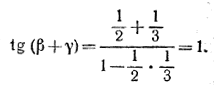
Отсюда β + γ= π/4 и α + β + γ= π/4 + π/4 = π/2





Похожие примеры:
В основании прямой призмы лежит прямоугольный треугольник с катетом а и противолежащим ему углом α. Через вершину прямого угла нижнего основания проведена плоскость, параллельная гипотенузе, под углом β= 90°— α к противолежащей боковой грани и пересекающая ее. Определить объем части призмы между ее основанием и сечением и боковую поверхность призмы, если известно, что боковая грань, проходящая через катет а, равновелика сечению призмы. Определить, при каком значении угла αплоскость сечения пересекает боковую грань, проходящую через гипотенузу основания. Смотреть решение→
Из точки А, расположенной внутри угла с зеркальными сторонами, исходит луч света. Доказать, что число отражений, которое испытывает этот луч от сторон угла, всегда конечно. Найти это число, если данный угол равен α, а луч направлен под углом β к одной из его сторон. Выяснить условия, при которых луч снова пройдет через точку А.  Смотреть решение→
В основании наклонной призмы лежит прямоугольный треугольник ABC с катетом ВС = а. Вершина В1верхнего основания проектируется на середину катета ВС. Двугранный угол, образованный боковыми гранями, проводящими через катет ВС и гипотенузу АВ, равен α. Боковые ребра наклонены к плоскости основания под углом β. Определить боковую поверхность призмы. Смотреть решение→