В основании пирамиды лежит равнобедренный треугольник с углом αпри основании. Каждый двугранный угол при основании равен φ = 90°— α. Боковая поверхность пирамиды равна S. Определить объем пирамиды и полную поверхность ее.
Согласно доказательству в задаче 425, Socн.
= S cos φ = S sin α. С другой стороны, ![]()
Приравнивая эти два выражения, получим a = 2√S cos α.
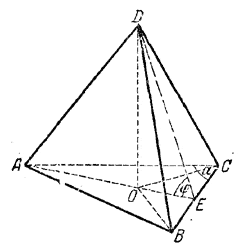
Точка О (центр окружности, вписанной в треугольник ABC; рис.) лежит на пересечении биссектрис углов треугольника, следовательно,
∠ OCE = α/2
и
OE = EC • tg α/2 = a/2 tg α/2
из \(\Delta\)DOE находим
H = OE• tg φ
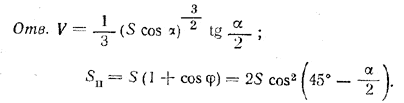
Похожие примеры: