Через данную точку O пространства провести прямую, перпендикулярную к данной плоскости P

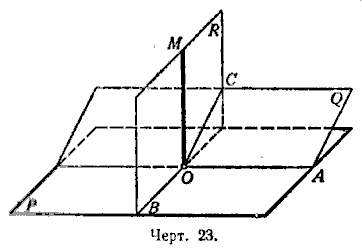
1-й случай. Точка О лежит на плоскости Р (черт. 23). Проведём на плоскости Р через точку О две какие-либо взаимно перпендикулярные прямые ОА и ОВ. Проведём, далее, через прямую ОА какую-либо новую плоскость Q и на этой плоскости Q построим прямую ОС, перпендикулярную к ОА. Через прямые ОВ и ОС проведём новую плоскость R и построим в ней прямую ОМ, перпендикулярную к ОВ. Прямая ОМ и будет искомым перпендикуляром к плоскости Р.

Действительно, так как ОА ⊥ ОВ и ОА ⊥ ОС, то прямая АО перпендикулярна к плоскости R и, следовательно, ОА ⊥ ОМ.
Таким образом, мы видим, что ОМ ⊥ ОА и ОМ ⊥ ОВ; следовательно, ОМ перпендикулярна к плоскости Р.

2-й случай. Точка О не лежит на плоскости Р (черт. 24).

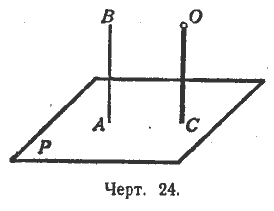
Возьмём на плоскости Р какую-нибудь точку А и выполним для неё предыдущее построение. Мы получим тогда прямую АВ, перпендикулярную к плоскости Р. После этого через точку О проводим прямую, параллельную АВ. Эта прямая и будет искомой.

Задача в обоих случаях имеет одно решение. В самом деле, так как два перпендикуляра к одной и той же плоскости параллельны, то через одну и ту же точку О нельзя провести двух перпендикуляров к плоскости Р. Следовательно, через каждую точку в пространстве можно провести одну и только одну прямую, перпендикулярную к данной плоскости.