Через данную точку C в пространстве провести плоскость, перпендикулярную к данной прямой AB

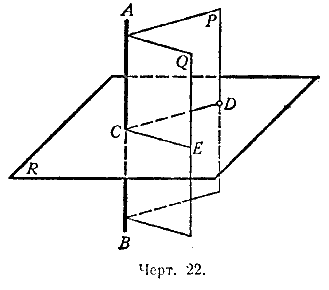
1-й случай. Данная точка С лежит на прямой АВ (черт. 22).

Проведём через прямую АВ какие-нибудь две плоскости Р и Q. Искомая плоскость должна пересекать эти плоскости по прямым, перпендикулярным к прямой АВ. Отсюда построение:
через АВ проводим две произвольные плоскости Р и Q.
В каждой из этих плоскостей восставляем перпендикуляр к прямой АВ в точке С (в плоскости Р - перпендикуляр СD, в плоскости Q-перпендикуляр СЕ).
Плоскость, проходящая через прямые CD и СЕ, есть искомая.

2-й случай. Данная точка не лежит на прямой АВ (черт. 22).

Через точку D и прямую АВ проводим плоскость Р и в этой плоскости строим прямую DC, перпендикулярную к АВ.
Через прямую АВ проводим произвольно вторую плоскость Q и в этой плоскости строим прямую СЕ, перпендикулярную к АВ.
Искомая плоскость должна пересечь плоскости Р и Q по прямым, перпендикулярным к АВ. Отсюда построение:
через точку D проводим в плоскости P прямую DС, перпендикулярную к АВ.
Прямая DС пересечёт прямую АВ в некоторой точке С.
Через точку С проводим в плоскости Q прямую СЕ перпендикулярную к АВ.
Плоскость, проходящая через прямые СD и СE - искомая.

Так как в каждой из плоскостей Р и Q через данную точку провести лишь, одну прямую, перпендикулярную к данной, то задача в обоих случаях имеет одно решение, т. е. через каждую точку в пространстве можно провести лишь одну плоскость, перпендикулярную к данной прямой.