Даны две скрещивающиеся прямые (a и b) и точка А, не лежащая ни на одной из данных прямых. Провести через точку А прямую, пересекающую обе данные прямые (a и b)

Так как искомая прямая должна проходить через точку А и пересекать прямую а, то она должна лежать в плоскости, проходящей через прямую а и точку А (так как две её точки должны лежать в этой плоскости: точка А и точка пересечения с прямой а). Совершенно так же убеждаемся, что искомая прямая должна лежать в плоскости, проходящей через точку А и прямую b . Следовательно, она должна служить линией пересечения этих двух плоскостей. Отсюда такое построение.
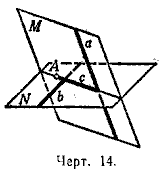
Через точку А и прямую а проводим плоскость М; через точку А и прямую b проводим плоскость N. Берем прямую с пересечения плоскостей М и N. Если прямая с не параллельна ни одной из данных прямых, то она пересечётся с каждой из данных прямых (так как с каждой из них она лежит в одной плоскости: а и с лежат в плоскости М, b и с - в плоскости N). Прямая с будет в этом случае искомой.
Если же а || с или b || с, то задача не имеет решения.