Даны две скрещивающиеся прямые a и b. Построить прямую, пересекающую обе данные прямые и перпендикулярную к ним обеим

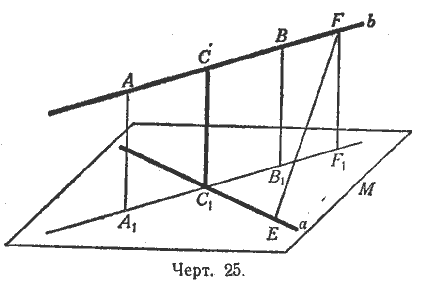
Проведём через прямую а плоскость М, параллельную прямой b. Из двух каких-нибудь точек прямой b опустим перпендикуляры АА₁ и ВВ₁ на плоскость М. Соединим точки А₁ и В₁ отрезком прямой и найдём точку С₁ пересечения прямых А₁В₁ и а. Через точку С₁ проведём прямую, перпендикулярную к плоскости М. Предоставляем самим учащимся доказать, что эта прямая: 1) пересечётся с прямой b в некоторой точке С и 2) будет перпендикулярна как к прямой а, так и к прямой b.

Прямая СС₁ будет, следовательно, искомой прямой.

Заметим, что отрезок СС₁ меньше всех других отрезков, которые можно получить, соединяя точки прямой а с точками прямой b. В самом деле, возьмём на прямой а какую-нибудь точку E и на прямой b какую-нибудь точку F , соединим эти точки отрезком прямой и докажем, что ЕF > СС₁.

Опустим из точки F перпендикуляр FF₁ на плоскость M, Тогда будем иметь:
ЕF > FF₁. Но FF₁ = CC₁, следовательно, EF > СС₁. На этом основании длина отрезка CC₁ называется кратчайшим расстоянием между данными прямыми а и b.