Вершины А, В и С треугольника соединены с точками А₁, В₁, С₁, расположенными произвольно на противоположных сторонах (но не в вершинах). Доказать, что середины отрезков AA₁, BB₁ и CC₁ не лежат на одной прямой.

Пусть A₂В₂, B₂С₂, С₂A₂— средние линии в \(\Delta\)АВС, А₃, В₃, С₃ — середины отрезков АА₁, ВВ₁, СС₁ .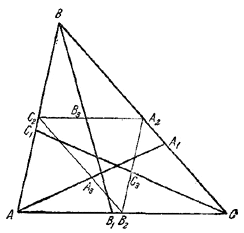

Точки А₃, В₃, С₃ лежат на средних линиях \(\Delta\)АВС и притом не на концах этих линий, так как, в противном случае, по крайней мере одна из точек A₁, B₁, С₁ совпала бы с вершиной \(\Delta\)АВС.

Так как всякая прямая, не проходящая через вершины треугольника A₂В₂С₂, не пересекает одновременно все три его стороны, то точки А₃, В₃, С₃ не лежат на одной прямой.