Через произвольную точку О, взятую внутри треугольника ABC, проведены прямые DE, FK, MN, параллельные, соответственно, AB, АС, BC, причем F и M лежат на AB, E и К - на BC, N и D - на АС, Доказать, что

$\frac{AF}{AB} + \frac{BE}{BC} + \frac{CN}{CA} = 1$

Если h₁ — высота $\Delta$DON, h_B — высота $\Delta$ABC, a S_АОC и S_ABC — площади соответствующих треугольников, то

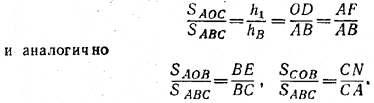
Сложив эти равенства, получим: