В треугольник вписан квадрат так, что одна из его сторон лежит на

В треугольник вписан квадрат так, что одна из его сторон лежит на наибольшей стороне треугольника. Доказать неравенство √2r < х < 2r , где х - длина стороны квадрата, r - радиус круга, вписанного в данный треугольник.

Рассмотрим окружность К' радиуса r', вписанную в квадрат, и проведем к ней касательные А'В' || АВ, В'С' || ВС.

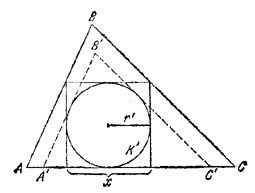
Ясно, что \(\Delta\)А'В'С' лежит внутри \(\Delta\)ABC, и поэтому А'С' < АС.

Так как

\(\Delta\)А'В'С' ~ \(\Delta\)ABC,

то \(\frac{r''}{r} = \frac{А'С'}{AC} < 1\), откуда х = 2r' < 2r.

2) Рассмотрим окружность К" радиуса r", описанную около квадрата, и проведем к ней касательные А"В" || АВ, В"С'' || ВС и А"C'' || АС (рис. 77).

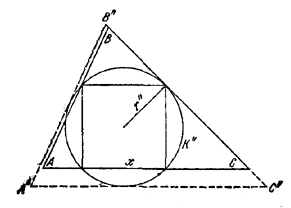
Pис. 77

Ясно, что \(\Delta\)ABC лежит внутри \(\Delta\) А"В"С" и поэтому А"С'' > АС. Так как

\(\Delta\) А"В"С'' ~ \(\Delta\) ABC,

то \(\frac{r"}{r} = \frac{А"С"}{AC} > 1\), откуда x = √2r" > √2r.