Параллельные стороны трапеции равны а и b. Определить длину отрезка, параллельного им и делящего площадь трапеции пополам.

Пусть отрезок EF = x делит площадь трапеции ABCD (AD = a, BC = b) пополам.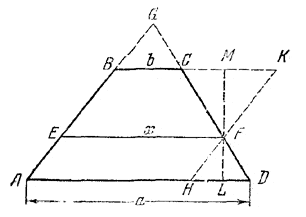

Тогда

т. е. (а + х) FL = (х + b) FM.

Высоты FL и FM по отдельности найти нельзя (длина одной из них может быть взята произвольно), но отношение FL : FM имеет определённую величину. Именно, из подобия треугольников HFD и CFK (где HD = a - х и СК = х- b) находим

Помножив почленно это равенство на предыдущее, получим

a² - х² = х² - b²

откуда

Другой способ. Продолжив боковые стороны, получим подобные друг другу треугольники ВGС, EGF и AGD. Их площади S₁, S₂, S₃ пропорциональны квадратам сходственных сторон b, х, а, так что S₁ = qb², S₂= qx², S₃ = qa², где q - некоторый коэффициент пропорциональности (величина его зависит от высоты трапеции).

По условию S₂-S₁= n = S₃ - S₂, т. е.

q(х² - b²)= q(a² - х²)

а так как q=/= 0, то х² - b² = a² - х²

Отв.