Из вершины тупого угла ромба опущены перпендикуляры на его стороны. Длина каждого перпендикуляра равна а, расстояние между их основаниями равно b. Определить площадь ромба.

По условию BE = BF = a и EF = b.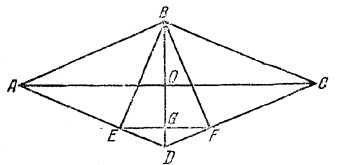

Значит, EG = ^b/₂ и . По теореме о пропорциональных линиях в прямоугольном треугольнике (BDE) находим

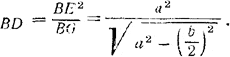
Теперь найдем сторону ромба (AD). Равнобедренные треугольники ABD и BEF подобны, так как их углы (все они острые) соответственно равны (как углы с взаимно перпендикулярными сторонами). Следовательно,

AD : BD = BE: EF, т. е,

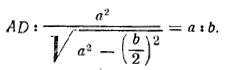
Отсюда находим AD, а затем площадь ромба S = AD • a.

Отв.