Определить площадь треугольника, если две стороны соответственно равны 27 см и 29 см, а медиана третьей стороны равна 26 см.

Пусть АВ =27 см и АС =29 см;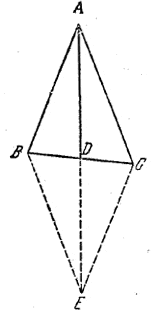

тогда медиана AD = 26 см. Продолжим AD на расстояние DE=AD. Четырехугольник АВЕС будет параллелограммом (доказать!) со сторонами 27 см и 29 см.

Площадь треугольника ABC составляет половину площади полученного параллелограмма, но и площадь треугольника ABE также составляет половину площади параллелограмма АВЕС. Следовательно, площадь треугольника ABC равна площади треугольника ABE, а стороны последнего известны (AB = 27 см; ВЕ = = 29 см; АЕ=52 см). Теперь площадь треугольника можно вычислить по формуле Герона:

S = √р(р - а)(р - b)(p - с)

Отв. 270 см².