Из точки О, лежащей в основании ABC треугольной пирамиды SABC, проведены прямые ОА', ОВ' и ОС', соответственно параллельные ребрам SA, SB, SC, до пересечения их соответственно с гранями SBC, SCA, SAB в точках А', В', С'. Доказать, что

^OA'/_SA + ^OB'/_SB+ ^OC'/_SC= 1

Пирамиды ASВС и OSBC имеют общее основание SBC (рис.), поэтому их объемы относятся как высоты, опущенные на их общее основание.

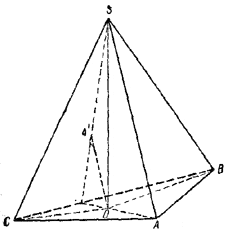
Так как ОА' || AS, то отношение высот пирамид ASBC и OSBC, опущенных на основание SBC, равно отношению SA к ОА'. Следовательно, отношение их объемов равно