Рассматриваются два треугольника ABC и А₁В₁С₁, которые лежат в непараллельных плоскостях и имеют попарно непараллельные стороны. При этом прямые, соединяющие соответственные вершины, пересекаются в одной точке О. Доказать, что продолжения соответственных сторон треугольников попарно пересекаются и точки их пересечения лежат на одной прямой.

Пусть Р есть плоскость треугольника ABC,
Р₁ - плоскость треугольника А₁В₁С₁, l - линия пересечения Р и Р₁.

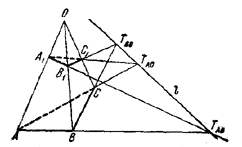
Обозначим через Q_AB плоскость, проходящую через А, В и О. Прямая А₁В₁ лежит в Q_AB и, будучи непараллельной прямой АВ, пересекается с ней в точке Т_AB. Эта точка лежит в плоскостях Р и Р₁ и, значит, на прямой l. Аналогично докажем, что прямые ВС и В₁C₁ пересекаются в точке Т_BC лежащей на l, а прямые АС и А₁C₁ - в точке Т_AC , лежащей также на l.