Показать, что отрезки, соединяющие вершины некоторой треугольной пирамиды с центрами тяжести противолежащих граней, пересекаются в одной точке и делятся этой точкой в отношении 1:3.

Пусть O₁ - центр тяжести грани ASC, ВО₁ - один из рассматриваемых в задаче отрезков. Возьмем еще какую-нибудь грань, например BSC; обозначим ее центр тяжести через О₂ и докажем, что отрезок АО₂ пересекает отрезок ВО₁ и при этом точка пересечения отрезков О делит отрезок ВО₁ в отношении 1:3, считая от точки О₁.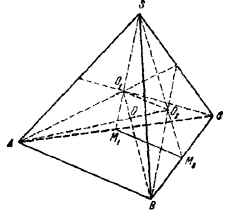

В самом деле, если M₁ и М₂ - середины отрезков АС и ВС (рис.), то очевидно, что АВ || М₁М₂ ; легко также видеть, что O₁O₂ || М₁М₂, так как точки О₁ и О₂ делят соответственно отрезки M₁S и M₂S в одном и том же отношении. Поэтому АВ || O₁O₂, фигура АВО₂О₁ - трапеция и, стало быть, ее диагонали ВО₁ и АО₂ пересекаются. Обозначим точку пересечения диагоналей через О.

Имеем:

Перемножив эти равенства, получим

Но из подобия треугольников AОВ и О₁ОО₂ следует Таким образом,

что и утверждалось.

Если мы теперь возьмем центр тяжести еще на одной грани и построим соответствующий отрезок, то он, в силу доказанного, также пересечет отрезок ВО₁ и притом в точке, которая разделит ВО₁ в отношении ¹/₃, т. е. в точке О. Следовательно, все рассматриваемые отрезки пересекаются в точке О. Очевидно также, что точка О делит любой из них в отношении 1:3, что и требовалось доказать.