На плоскости лежат четыре равных шара радиуса R, причем три из них касаются попарно друг друга, а четвертый касается двух из этих трех. На эти шары сверху положены два равных шара меньшего радиуса, касающихся друг друга, причем каждый из них касается трех больших шаров. Найти отношение радиусов большого и малого шаров.

Пусть А, В, С, D - центры больших шаров. Рассмотрим проекцию всех шаров на плоскость А, В, С, D.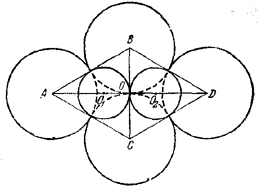

Так как центры малых шаров равноудалены от центров соответствующих больших шаров, они спроектируются в центры тяжести O₁ и О₂ равносторонних треугольников ABC и BCD. Так как, кроме того, радиусы малых шаров по условию равны, то отрезок, соединяющий их центры, параллелен рассматриваемой плоскости и делится точкой касания шаров пополам. Ввиду этого проекция точки касания окажется на отрезке BC. Отсюда следует, что малые шары спроектируются в круги, вписанные в треугольники ABC и BCD. Поэтому радиус малых шаров равен