На плоскости лежат три равных шара радиуса R, попарно касающихся друг друга. Четвертый шар касается плоскости и каждого из первых трех шаров. Найти радиус четвертого шара.

Пусть А, В, С - центры шаров радиуса R, А₁, B₁, C₁ - проекции этих центров на плоскость, О - центр четвертого шара, радиус r которого нужно найти.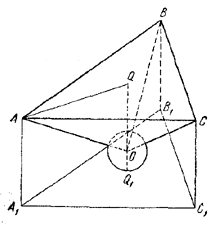

Соединив центры всех шаров, мы получим, очевидно, правильную треугольную пирамиду ОАВС, у которой AB = BC = AC = 2R, АО = ВО = СО = R + r, OQ = R - r. Отрезок AQ есть радиус описанной около \(\Delta\)ABC окружности, поэтому

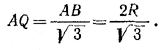
Из треугольника AQO по теореме Пифагора находим:

Решив это уравнение, получаем r= ^R/₃.