В правильную четырехугольную пирамиду вписан полушар так, что плоская грань его лежит на основании пирамиды, а шаровая поверхность касается боковых граней пирамиды. Найти отношение полной поверхности полушара к полной поверхности пирамиды и объем полушара, если боковые грани наклонены к плоскости основания под углом α и разность между стороной основания и диаметром шара равна m.
Плоскость ESF (рис.) даст в пересечении с полушаром полукруг NPM, касающийся апофем пирамиды (в точках Q и G).
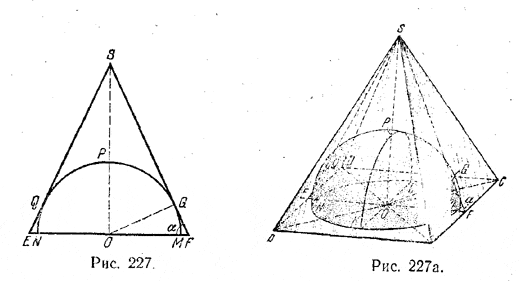
Если обозначим сторону основания пирамиды через а, а радиус полушара - через r, то полная поверхность полушара S1 будет
S1 = 2πr2 + πr2 = 3πr2
и полная поверхность пирамиды
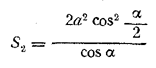
их отношение
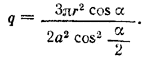
Из \(\Delta\)OGF имеем OG = OF• sin α, т. е. r = a/2 sin α. Это выражение подставим в предыдущее равенство.
Для вычисления объема полушара V найдем r из условия а - 2r = m и ранее найденного равенства r = a/2 sin α. Получим
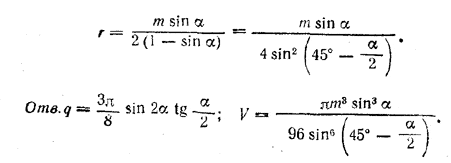
Похожие примеры: