В правильную четырехугольную пирамиду вписан полушар так, что его плоская грань параллельна основанию пирамиды, а шаровая поверхность касается его. Определить полную поверхность пирамиды, если боковые ее грани образуют с основанием угол αи радиус шара равен r.
Центр О экватора полушара (т. е. круга, ограничивающего полушар; рис.) лежит па высоте SO1 пирамиды.
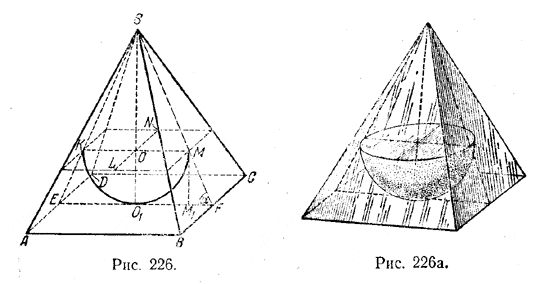
Так как
OM = OO1 = r ,
то точка М лежит на биссектрисе О1М угла ОО1М1. Отметив точку М как пересечение O1М с SF, изображаем сечение KLMN, параллельное основанию. Середины К, L, М, N сторон сечения являются точками касания экватора с боковыми гранями. Полукруг КО1М есть сечение полушара плоскостью ESF.
Решение. Сторона основания а равна
a = EF = 2 • O1F = 2 (O1M1+M1F).
Но O1M1 = OM = r, a M1F = MM1 • ctg α = r ctg α. Значит,
a = 2r (1+ctg α).
Имеем

Здесь Socн. = а2 = 4r2 (1+ctg α)2 .
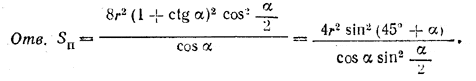
Похожие примеры: