В треугольнике даны стороны b и с и угол между ними α. Этот треугольник вращается около оси, которая проходит вне его через вершину угла α и равно наклонена к сторонам b и с. Определить объем тела вращения.
Объем V (рис.) тела вращения равен объему усеченного конуса, полученного от вращения трапеции ОО1ВС, без объема двух конусов, полученных от вращения треугольников АО1В и АОС.
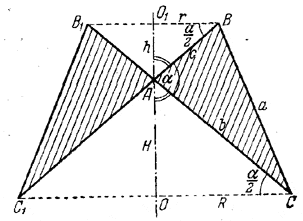
Так как по условию ∠ BAO1 = ∠ CAO, то ∠ BAO1 = ∠ CAO = 90° - α/2 так что
∠ O1BA = ∠ OCA = α/2.
При обозначениях рис. имеем Н = b sin α/2 , R = b cos α/2 (из треугольника АОС) и h = с sin α/2 , r = с cos α/2 ; (из треугольника АО1В), Значит,
V = π/3 (H + h) (R2 + Rr + r2) - π/3 HR2 - π/3 hr2=
= π/3 sin α/2 cos2 α/2 [( b + c ) (b2 + bc + c2) - b3 - c3].
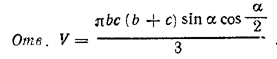
Похожие примеры: