Ромб с большей диагональю d и острым углом γвращается вокруг оси, проходящей вне его через вершину ромба и перпендикулярной к большей диагонали его. Определить объем тела вращения.
Объем тела вращения (сечение его изображено на рис.) равен сумме объемов двух равных усеченных конусов, полученных от вращения трапеций AMВС и ANDC, без суммы объемов двух равных конусов, полученных от вращения треугольников AMВ и AND.
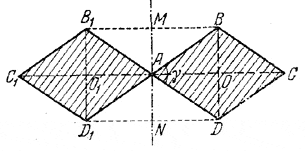
Радиус одного основания усеченного конуса АС = d , а другого МВ = d/2. Имеем
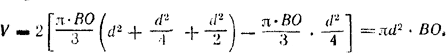
Из \(\Delta\)АОВ находим
BO = d/2 tg γ/2.
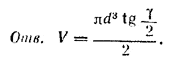
Похожие примеры: