В шар радиуса R вписана прямая треугольная призма. Основанием призмы служит прямоугольный треугольник с острым утлом α, и наибольшая ее боковая грань есть квадрат. Найти объем призмы.

Плоскости оснований (ВАС и В₁А₁С₁ на рис.) призмы пересекают шар по окружностям.

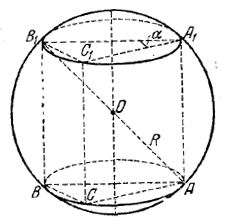
Прямоугольные треугольники ABC и A₁B₁C₁ вписаны в эти окружности. Поэтому гипотенузы АВ и A₁B₁ являются диаметрами окружностей. Плоскость AВB₁A₁ проходит через центр шара. Так как по условию AВB₁A₁ есть квадрат, то H = AA₁= R√2 и AB = R√2 .