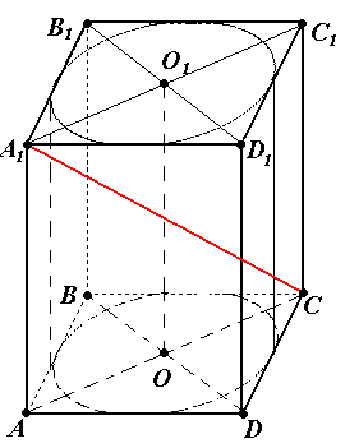
1) Так как цилиндр вписан в призму, то высота призмы равна высоте цилиндра, а основание цилиндра вписано в основание призмы.

2) Так как радиус окружности, описанной вокруг основания призмы, равен R = 2√2, то сторона квадрата равна a = R√2 = 2√2 * √2 = 4 а радиус цилиндра равен радиусу вписанной в квадрат окружности и равен: \(r=\frac{a}{2}=2\)

3) По условию объём цилиндра равен \(16\pi \sqrt2\), т.е. \(\pi r^2 H = 16\pi \sqrt2, H = \frac{16\sqrt2}{r^2} =4\sqrt2\) .

4) Из прямоугольного треугольника \(АСА_1\) находим диагональ \(А_1С\) :
\(А_1С = \sqrt{H^2 + (2R)^2} = \sqrt{32+32} =\sqrt{64} =8\).

Ответ: 8