Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20π. Найдите площадь боковой поверхности призмы.

$$ S = P \cdot H $$

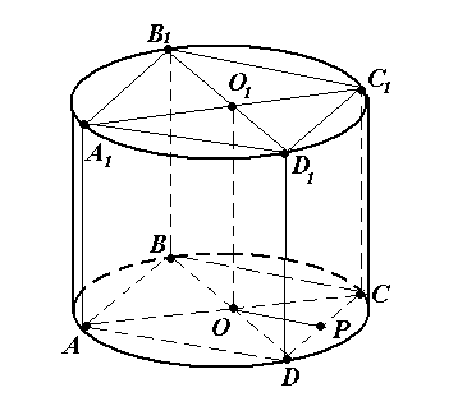
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра.

2) По условию площадь боковой поверхности цилиндра равна 20π, т.е. \( 2\pi RH = 20\pi, RH = 10\).

3) так как призма правильная, то в её основании лежит квадрат со стороной a=R√2, тогда периметр основания равен 4R√2.

4) вычислим площадь боковой поверхности призмы S = P * H = 4R√2 * H = 4√2 * RH = 4√2 * 10 = 40√2.

Ответ: 40√2