В треугольную пирамиду, в основании которой — правильный треугольник со стороной а, вписан цилиндр так, что нижнее его основание находится на основании пирамиды, а верхнее касается всех боковых граней. Определить объем цилиндра и объем пирамиды, отсеченной плоскостью, проходящей через верхнее основание цилиндра, если известно, что высота цилиндра равна a/2, одно из боковых ребер пирамиды перпендикулярно к плоскости основания, а боковая грань наклонена к основанию под углом α (определить, при каких значениях а задача возможна).
Радиус R = OF (рис.) цилиндра равен 1/3 BF
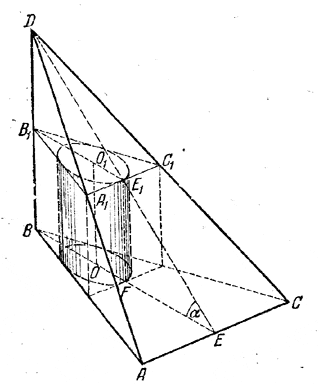
Но
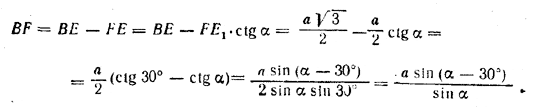
Поэтому объем цилиндра
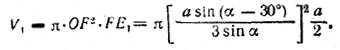
Объем V2 пирамиды DA1B1C1 равен
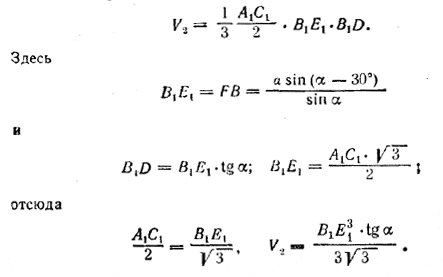
Задача возможна при условии, что BE > BF, т. е. при условии ![]() или ctg 30° > ctg α; следовательно, α > 30° ,
или ctg 30° > ctg α; следовательно, α > 30° ,
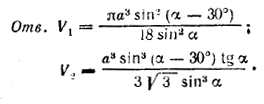
Похожие примеры: