Даны отрезок АВ и на нем точка С. Каждая пара равных окружностей, одна из которых проходит через точки А и С, а другая - через точки С иВ, имеет, кроме С, еще одну общую точку D. Найти геометрическое место точек D.

Искомое геометрическое место есть перпендикуляр к отрезку АВ, проведенный через его середину Е, с выброшенной точкой Е.

Доказательство. Треугольник ADB - равнобедренный, так как ∠CAD = ∠CBD, ибо эти углы опираются в равных окружностях на равные дуги CD (рис.).

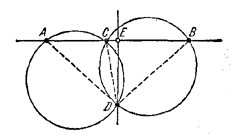
Поэтому точка D лежит на перпендикуляре к отрезку АВ, проведенному через его середину Е. Наоборот, если взять любую точку D на этом перпендикуляре, не совпадающую с точкой Е, то окружности, проходящие через ACD и BCD, равны. Это следует, например, из равенств

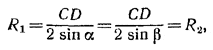
где α = ∠BAD и β = ∠CBD.