Стороны деформирующегося многоугольника остаются соответственно параллельными заданным направлениям, в то время как все вершины, кроме одной, скользят по заданным прямым. Найти геометрическое место положений последней вершины.

Искомое геометрическое место есть прямая, проведенная через какие-нибудь два различных положения последней вершины.

Доказательство. Пусть, например, A₁В₁С₁D₁E₁ - одно и A₂В₂С₂D₂E₂ - другое положения деформирующегося многоугольника, вершины А, В, С, D которого скользят соответственно по прямым l_A, l_B, l_C, l_D, (рис.).

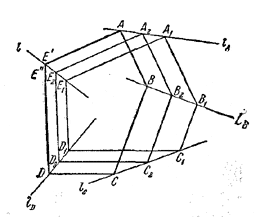
Через положения Е₁ и E₂ последней вершины проведем прямую l. Пусть вершина на прямой l_A заняла положение А, а на l_D - соответствующее положение D. Сторона, параллельная A₂E₂, пересечет l в точке E', а сторона, параллельная D₂E₂ ,- в точке Е". По построению

откуда

E'E₂ = E''E₂

т. е. точки E' и E" совпадают. Это означает, что последняя вершина будет лежать на прямой l в точке Е = Е' = E".

Обратное очевидно, так как положение деформированного многоугольника можно построить, начиная с любой точки Е на прямой l.