В прямоугольник со сторонами 3 м и 4 м вписан другой прямоугольник, стороны которого относятся, как 1 : 3. Найти стороны этого прямоугольника.

Предварительное замечание. Из решения выяснится, как отыскать положение вершин вписанного прямоугольника KLMN. Пока нужно выполнить построение схематически, начав с построения прямоугольника KLMN.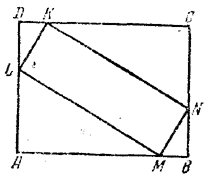

Решение. Найдем отрезки МВ = х и BN = y. Так как AB= 4, то AM = 4 - х. Треугольники DLK и BNM равны (доказать!); следовательно, DL= BN = y и LA=3-y. Трeугольники LAM и MNB подобны, ибо острые их углы ALM и NMB равны (как углы с взаимно перпендикулярными сторонами). А так как по условию ML втрое больше, чем MN, то и LA = 3MB, а также AM = 3BN, т. е. 3 - у = 3х и 4 - х = 3у.

Отсюда находим х = ⁵/₈у = ⁹/₈. Теперь имеем

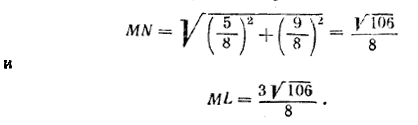
Отв. Стороны прямоугольника равны

^√106/₈ ≈ 1,29 м и ^3√106/₈≈ 3,87 м