В равносторонний треугольник ABC, сторона которого а, вписан другой равносторонний треугольник LMN, вершины которого лежат на сторонах первого треугольника и делят каждую из них в отношении 1:2. Определить площадь треугольника LMN.

Площадь равностороннего треугольника ABC равна ¹/₂а • ^√3/₂ а = ^√3/₄ а².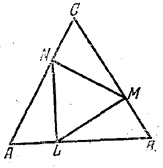

рис.7

Треугольник ANL, у которого по условию AL= ¹/₃а и AN = ²/₃а , имеет общий угол А с треугольником ABC. Значит, их площади относятся как произведения сторон:

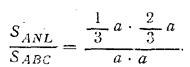
Поэтому

S_ANL = ¹/₃ • ²/₃S_ABC= ²/₉S_ABC

Следовательно,

Замечание. Треугольник LMN, равно как и треугольник ABC, равносторонний (доказать). По тем же способом можно определить площадь треугольника LMN в общем случае, когда треугольник ABC произвольный и стороны его разделены в произвольных отношениях.