Стороны квадрата разделены в отношении m к n, причем к каждой вершине прилежит один большой и один малый отрезок. Последовательные точки деления соединены прямыми. Найти площадь полученного четырехугольника, если сторона данного квадрата равна а.

По условию задачи отрезок АВ = а делится точкой М в отношении m:n.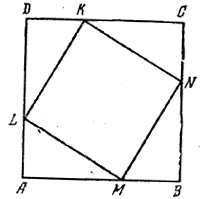

Поэтому
Таким же образом

Следовательно,

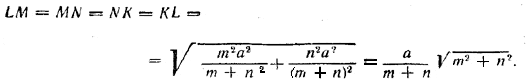
Кроме того, все углы четырехугольника LMNK прямые (ибо из равенства треугольника ALM и BMN имеем ∠LMA- ∠MNB = 90° - ∠NMB; следовательно, ∠LMA + ∠NMB = 90°; поэтому ∠LMN = 90°). Значит, четырехугольник LMNK есть квадрат.

Другое решение. Из площади квадрата ABCD вычитаем общую площадь четырех треугольников.