На сторонах равнобедренного прямоугольного треугольника с катетом b построены квадраты во внешние стороны. Центры этих квадратов соединены между собою прямыми линиями. Найти площадь получившегося треугольника.

Пусть ABC есть данный треугольник (АС = СВ = b), Требуется определить площадь S треугольника О₁О₂О₃.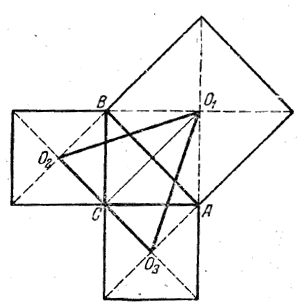

Имеем S = ¹/₂ О₂О₃ • O₁C, где О₂О₃=АВ и O₁C = AB. Следовательно,

S= ¹/₂ AB²= b²

Другое решение. Треугольник О₁О₂С равновелик треугольнику О₁ВС (у них общее основание О₁и равные высоты). Треугольник О₁О₃С равновелик треугольнику О₁AC (пo той же причине). Значит, треугольник О₁О₂О₃ равновелик квадрату О₁ВСА.

Отв. S = b².