Некоторая точка О плоскости соединена с вершинами параллелограмма ABCD. Доказать, что площадь треугольника АОС равна сумме или разности площадей двух смежных треугольников, образованных двумя из прямых ОА, ОВ, ОС, OD и соответствующей стороной параллелограмма. Разобрать случаи, когда точка О находится внутри и вне параллелограмма.

Обозначим через h_B, h_C и h_Dрасстояния от вершин В, С и D параллелограмма до прямой АО.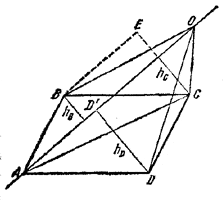

Тогда имеет место следующее свойство: наибольшее из этих трех расстояний равно сумме двух других. Например, если АО пересекает сторону ВС, то, проведя BE || АО и CE ⊥ AO, из равенства треугольников ВЕС и AD'D найдем:

h_D = h_B + h_C

Аналогично, если АО пересекает сторону CD то h_B = h_C+ h_D, если АО не пересекает сторон ВС и CD, то h_C= h_B+ h_D. Из этого свойства для случая, показанного на рис., сразу следует равенство для площадей треугольников:

S_AOC = S_AOD — S_AOB

Вообще, очевидно, можно написать формулу

S_AOC =| S_AOD ±S_AOB |

где берется знак плюс, если точки В и D лежат по одну сторону от АО, и знак минус, если точки В и D лежат по разные стороны от АО.

Повторение этого рассуждения для прямой СО вместо АО приводит к аналогичной формуле

S_AOC =| S_COD ±S_COB |

с тем же правилом выбора знаков, но относительно прямой СО.