На сторонах АВ, АС, ВС треугольника ABC, как на основаниях, построены три равнобедренных подобных треугольника АВР, ACQ, ВСR, два первых - вне данного треугольника, третий - по ту же сторону, что и данный треугольник. Доказать, что APRQ — параллелограмм (или что точки А, Р, R, Q лежат на одной прямой).

В обозначениях рис. 85 имеем:

∠PBR = ∠ABC

и

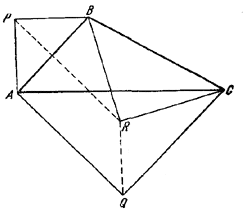
Pис. 85

Поэтому \(\Delta\)PBR ~ \(\Delta\)ABC и аналогично \(\Delta\)QRC ~ \(\Delta\)ABC. Пользуясь этим, получим:

∠APR = ∠APB — ∠BPR = ∠APB — ∠BAC,

поэтому

∠APR + ∠PAQ = ∠APB + 2 ∠РАВ = π,

так что PR || AQ. Аналогично докажем, что QR || АР.