Рассматриваем куб с ребром а. Через концы каждой тройки ребер, выходящих из общей вершины, проведена плоскость. Найти объем тела, ограниченного этими плоскостями.
Полученное тело есть октаэдр, вершины которого находятся в центрах симметрии граней куба.
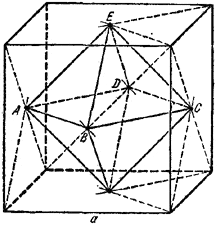
Объем октаэдра равен удвоенному объему правильной четырехугольной пирамиды EABCD высоты a/2 с площадью основания ABCD, равной 1/2 а2. Следовательно, искомый объем равен
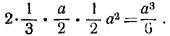
Похожие примеры:
Над плоским потолком зала, имеющего форму квадрата со стороной а, сделана крыша, построенная следующим образом: каждая пара смежных вершин квадрата, образующего потолок зала, соединена прямыми с серединой противолежащей стороны, на каждом из получившихся четырех треугольников, как на основании, построена пирамида, вершина которой проектируется в середину соответствующей стороны квадрата. Расположенные выше других части граней этих четырех пирамид образуют крышу. Найти объем чердака (т. е. пространства между потолком и крышей), если высота каждой из пирамид равна h. Смотреть решение→

![]()