Конус с высотой Н и углом между образующей и высотой, равным α, надо рассечь сферической поверхностью с центром в вершине конуса так, чтобы объем конуса оказался разделенным пополам. Найти радиус этой сферы.
По условию задачи объем V шарового сектора CMKN (рис.) должен составлять половину объема конуса АСВ.
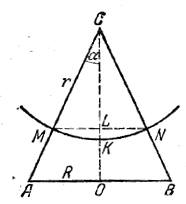
Обозначим отрезок KL через h, а высоту конуса СО через Н. Тогда V = 2/3 πr2h. Получаем равенство 2/3 πr2h = 1/2•1/3 πR2H; т. е. 4r2h = R2H или 4r2h = H3 tg2 α. Величину h выразим через r. Имеем
h = LK = СK- CL = r - r cos α = 2r sin2 α/2.
Получаем уравнение
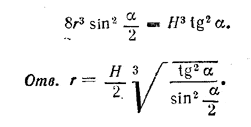
Похожие примеры: