Определить угол между высотой и образующей конуса, боковая поверхность которого делится на две равновеликие части линией пересечения ее со сферической поверхностью, имеющей центр в вершине конуса и радиус, равный высоте конуса.

По условию боковая поверхность конуса MCN (рис.) должна составлять половину боковой поверхности конуса АСВ. Но боковые поверхности этих конусов относятся, как квадраты образующих, т. е.

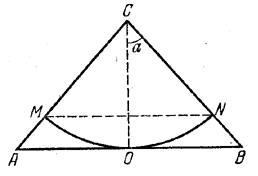
А так как CN = CO, то 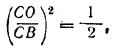т. е. cos² α = ¹/₂

Ответ: α = 45°.