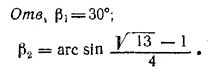Определить угол между высотой и образующей конуса, если известно, что объем конуса в 1¹/₃ раза больше объема полушара, вписанного в конус так, что плоская грань полушара лежит в основании конуса, а полушаровая поверхность касается боковой поверхности конуса.

При обозначениях предыдущей задачи имеем соотношение ^π/₃R²H = ⁴/₃•²/₃ πr³. Обозначим искомый угол через β (на рис. β = ^α/₂). Тогда r = R cos β и H = R ctg β. Из предыдущего соотношения получим 3ctg β - 8 cos³ β = 0. Помножив обе части этого уравнения ни tg β (эта величина по смыслу задачи не может равняться нулю), получим уравнение

3 - 8sin β cos² β = 0,

откуда

8 sin³ β -8 sin β + 3=0.

Для решения этого кубического уравнения придется применить какой-либо искусственный прием. Так, левую часть удается разложить на множители:

8 sin³ β -8 sin β + 3 = (8 sin³ β - 1) - (8 sin β - 4) =

= [(2sin β)³-1] - 4 (2 sin β - 1) = (2 sin β - 1) [(2 sin β)²+2 sin β + 1- 4].

Следовательно, найденное уравнение распадается на два.

Из первого находим sin β = ¹/₂ , а из второго (Другое

решение квадратного уравнения не годится.) Проверка показывает, что оба найденных решения годны.