Через вершину конуса проведены две плоскости. Одна из них наклонена к плоскости основания конуса под углом α и пересекает это основание по хорде, длина которой равна а, а другая наклонена к плоскости основания под углом β и пересекает основание по хорде, длина которой равна b. Определить объем конуса.
Вращая данные плоскости вокруг высоты конуса, не изменяя углов α и β, можно привести их в положение (изображенное на рис.), чтобы они пересекались друг с другом по общей образующей BD конуса.
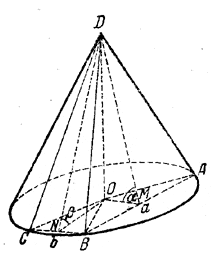
рис.
Из треугольников ОВМ и OBN находим
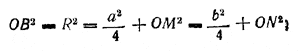
здесь ОМ = Н ctg α и ON = H ctg β. Следовательно,
![]()
Из этих уравнений находим H и R.
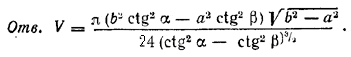
Похожие примеры: