Внутри равностороннего треугольника взята произвольная точка, из которой опущены перпендикуляры на все его стороны. Доказать, что сумма этих трех перпендикуляров равна высоте треугольника.

Пусть О - произвольная точка внутри равностороннего треугольника ABC.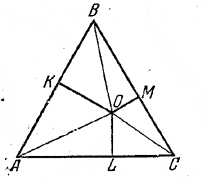

Соединим точку О с вершинами. Площади треугольников АОВ, BОС и СОА в сумме дадут площадь треугольника ABC. Обозначая сторону этого треугольника через а, а высоту через h, получим

(OK + OL + OM) ^a/₂ = ^ah/₂.

Отсюда находим

h = OK + OL + OM.