В параллелограмме проведены биссектрисы внутренних углов до взаимного пересечения. Доказать, что четырехугольник, образованный этими биссектрисами, - прямоугольник.

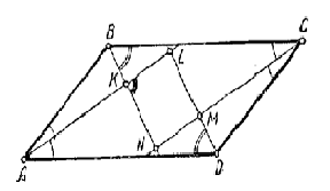
∠LAD = ∠NCB и ∠NBC = ∠LDA, как половины равных углов, а потому треугольники BCN и DAL равны, откуда AL = CN и BN = DL.

Аналогично АК = СМ и ВК = DМ. Тогда KL = MN и KN = LM, как разности равных отрезков.

Внешний угол треугольника АВК ∠АКN = ∠АВК + ∠ВАК = 90°, и потому ∠NKL = 90°; следовательно, четырехугольник KLMN – прямоугольник.